Objetivo: 173 escaños

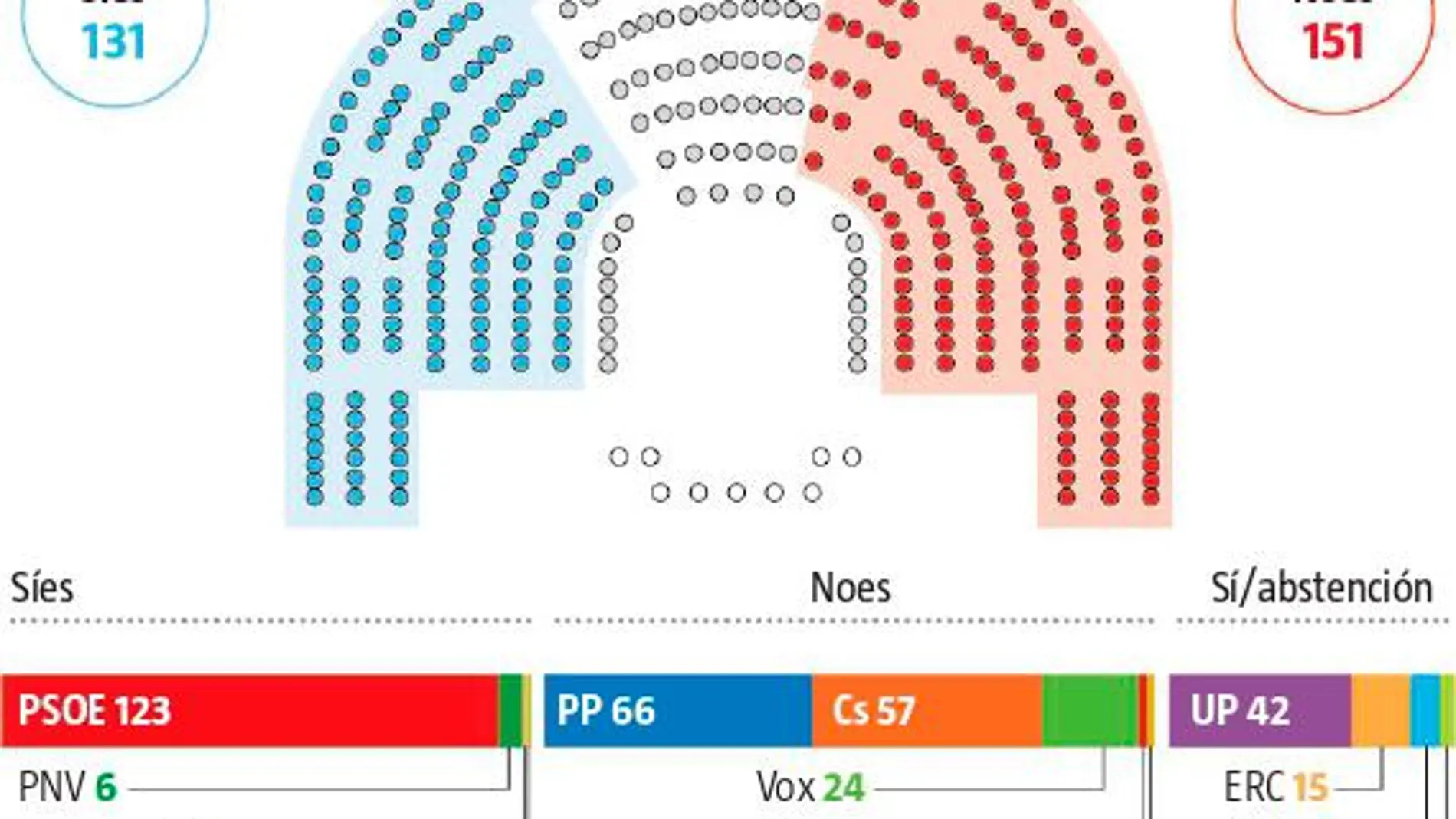
¿En qué aritmética confía Moncloa para lograr un segundo mandato para Pedro Sánchez?

Desde el primer momento Sánchez proyectó una investidura «tranquila» con el apoyo de Unidas Podemos (42), PNV (6), el Partido Regionalista de Cantabria (1) y Compromís (1), que sumados a los 123 con los que cuenta el partido del presidente en funciones dan la «mágica» cifra de 173 votos afirmativos. Tal y como está configurado el reparto de escaños en el Congreso de la XIII Legislatura sería poco menos que imposible que con estos apoyos se le escapara a Sánchez revalidar el cargo.

¿Sería necesaria la abstención de los independentistas si Unidas Podemos apoya finalmente a Sánchez?

Si finalmente se firma un pacto con el partido morado el número de «síes» sería, como se apuntó, 173. El número de votos negativos de PP (66), Ciudadanos (57), Vox (24), Navarra Suma (2) y Coalición Canaria (2) suma 151 escaños. A dos aguas quedarían los votos de los partidos independentistas, que suman en total 26 a los que hay que descontar los cuatro diputados presos (Oriol Junqueras, de ERC; y Jordi Sànchez, Jordi Turull y Josep Rull, de Junts per Catalunya) por lo que estaríamos hablando de 22 votos efectivos. Si todos ellos en bloque votan «no» se llegaría a un empate a 173 que no lograría que Pedro Sánchez fuera investido. Por lo tanto es necesario que al menos uno de los tres partidos independentistas se abstenga.

¿Es factible que tanto Bildu como JxCat como ERC voten negativamente?

Es muy improbable. De hecho Esquerra ya ha informado de que si Sánchez se presenta a la investidura con un acuerdo firmado con Unidas Podemos la formación republicana se pasaría a la abstención. «Por nosotros no va a ser», dijo literalmente Gabriel Rufián. Si esto fuera así y Bildu y JXCat votan «no», la investidura saldría adelante con 173 a favor, 161 en contra y 12 abstenciones. Sin embargo, es más que probable que alguna otra formación independentista se pase también a la abstención.