Hace ya más de un año que la pandemia de COVID-19 llegó a España y, desde entonces, hemos buscado un espejo en el que mirarnos. Hemos tratado de compararnos con el resto de los países, intentando discernir si estábamos tomando las decisiones adecuadas o si se nos estaba escapando algo. ¿Cómo es posible que nuestras medidas parecieran no surtir efecto? Entre el alboroto, algunos expertos en epidemiología trataron de alzar la voz. Advirtieron sobre los problemas que conlleva comparar a la ligera dos ciudades o países. Su mensaje no caló demasiado en la población general, pero llevaban razón.

No hay dos países iguales y dentro de ellos, cada ciudad tiene sus peculiaridades. Algunas están mejor conectadas, otras tienen una mayor densidad poblacional, cambia incluso el tipo de ocio que practican sus habitantes. Todo esto influye en cómo se transmite una enfermedad. Por ejemplo, una cultura en la que apenas se pasa tiempo en espacios cerrados podría ser menos propensa a producir supercontagiadores. Si pretendemos entender cómo evoluciona una epidemia tenemos que ser capaces de cuantificar estos aspectos diferenciadores para aislar el verdadero impacto que estén teniendo las medidas adoptadas por sus gobiernos. La pregunta es cómo y parece que la respuesta viene de la mano de las matemáticas.

Sociedades inconmensuables

Es relativamente sencillo cuantificar algunos aspectos de la realidad. Por ejemplo, el número de habitantes de una ciudad. Puede ser más o menos complejo contarlos a todos, pero sabemos que si lo conseguimos tendremos exactamente el dato que buscamos. Podemos valorar también la densidad de población, simplemente dividiendo el total de habitantes entre la superficie que ocupa su ciudad. Lo mismo ocurre con el salario mediano, la edad media, etc. Sin embargo, otros aspectos de la realidad se vuelven algo más difusos. Por ejemplo: las medidas de saneamiento de una ciudad, su clima, las conexiones que establece con otras ciudades.

Puede parecer engañosamente sencillo, pero si nos paramos a pensarlo, por mucho que podamos contar cuántas carreteras de cuántos carriles parten de una ciudad hacia el exterior, también tendremos que ponderar las vías de ferrocarril, los vuelos, etc. ¿Qué cuenta más? ¿Una línea de tren o una autopista? Si tratamos de reducirlo al número de personas que entran y salen también tendremos un problema, pues no estamos igual de expuestos en un viaje en coche que el vagón de un tren. Y podemos rizar el rizo una vez más, porque por poder, puede afectar incluso con qué ciudades esté conectada la nuestra: ¿son grandes?, ¿tienen a su vez muchas conexiones con terceras ciudades? En estos casos es harto difícil reducir la realidad a un único número, como ocurría con la densidad de población.

Esto no significa que sea imposible, solo que hay que encontrar la forma de medirlo que resulte más útil para nuestros propósitos: entender cómo se propaga una enfermedad infecciosa. Claro que, mientras tanto, nos las tendremos que ver con cientos de miles de ciudades, cada una con su idiosincrasia y con infinidad de características difíciles de cuantificar. Y esta es la clave, porque hasta que no podamos cuantificar las características más determinantes, las distintas poblaciones permanecerán inconmensurables o, dicho de otro modo: no podremos comparar unas ciudades con otras.

Un nuevo modelo

No obstante, son muchos los trabajos que, durante el último año, han avanzado brillantemente en esta línea. Un nuevo modelo parece haber encontrado una solución suficientemente buena como para predecir el modo en que se comportará una ciudad ante la infección. Cuando hablamos de modelos matemáticos nos referimos a fórmulas que permiten darle un valor a cada una de las principales características que definen aquello que queremos estudiar: población, conexiones, clima, etc. Al hacerlo, tan solo tenemos que sustituir estas características por aquello que hayamos medido y el modelo nos entregará una suerte de predicción.

Cabe destacar que, como dijo George Edward Pelham, “todos los modelos están equivocados, pero algunos son útiles”. Con ello, pretendía decir que los modelos son “caricaturas” de la realidad, no representan cada detalle de aquello que pretendemos estudiar porque, sencillamente, no sería posible gestionar tanta información en tantas variables diferentes. La meta no es el hiperrealismo, sino el encontrar un conjunto mínimo de características suficientemente determinantes como para obtener un modelo relativamente sencillo pero capaz de predecir la realidad con suficiente éxito.

Una forma de visualizarlo es retrotraernos a aquellos confusos primeros meses de la pandemia en nuestro país. Por aquel entonces estaba de moda el término “exponencial” y se decía con frecuencia que así es como crecía el número de infectados. Un crecimiento exponencial es aquel que aumenta multiplicándose por un número (2, 4, 8, 16, 32…) lo cual significa que sus valores despegan a toda velocidad. En los primeros momentos, construir un modelo de crecimiento exponencial podía ser útil, pero nada sigue ese ritmo para siempre. Existen multitud de factores que limitan el avance de una pandemia y que hay que tener en cuenta si pretendemos utilizar el modelo para estudiarla a largo plazo. Así es como se empezó a hablar de funciones logísticas, las cuales representaban un crecimiento inicialmente exponencial, pero que pronto llegaba a una suerte de meseta de la cual no pasaba. Una vez más, se trataba de un modelo “de juguete” y los verdaderos expertos sabían que hacía falta complicarlo un poco más para desatar su verdadero potencial.

Así pues, nos encontramos un segundo desafío a la hora de construir un modelo capaz de predecir cómo se comportarán las ciudades y, por lo tanto, que nos permita compararlas y entender cómo afectan realmente las medidas políticas. Por un lado, hemos de descubrir cómo cuantificar las variables más importantes, por otro, hemos de saber cuáles son exactamente esas variables imprescindibles para dotar de utilidad al modelo.

Los dos ejes del problema

Hasta ahora, la mayoría de los estudios que se habían enfrentado a este reto habían tratado de tener en cuenta o bien la conectividad de las ciudades, o bien la idoneidad de sus características respecto al ciclo de vida del patógeno. Pocos habían tratado de aunar ambos aspectos en un mismo modelo y esa es precisamente la línea de investigación en la que han estado trabajando desde la Universidad de Maine, tanto Brandon Lieberthal como Allison Gardner. Su trabajo ha sido recientemente publicado en la revista PLOS Computational Biology.

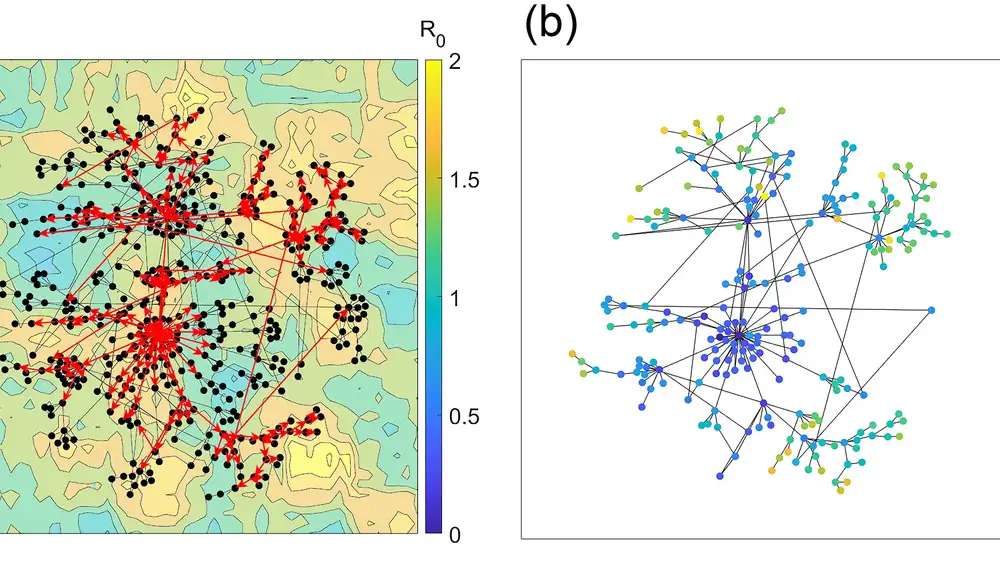
El modelo de Lieberthal y Gardner pretende descubrir qué ciudades tienen más probabilidades de convertirse en focos críticos de una enfermedad infecciosa. Como hemos dicho, para ello han tenido en cuenta la interconectividad entre ciudades, así como otro aspecto al que han denominado “idoneidad para la infección”. Esto último es un conjunto de variables complejas que tienen en cuenta aspectos como las condiciones meteorológicas, el alcantarillado, etc.

Gracias a este modelo, por ejemplo, empezamos a entender que el riesgo de que una ciudad se vuelva supercontagiadora aumenta a medida que se sus características se vuelven más idóneas para la infección, pero solo hasta cierto punto, a partir de esa cota el riesgo no crece. Ese límite, en cambio, no parece estar presente cuando valoramos la conectividad, la cual semeja crecer sin límite a medida que aumenta la interconectividad de una ciudad.

Visto así, podemos defender con datos la evidencia que llevamos meses percibiendo. Que, por ejemplo, sean tan difíciles de controlar los brotes de grandes ciudades como Madrid y Barcelona puede explicarse parcialmente mediante este nuevo modelo, debido a la enorme interconectividad de estas dos ciudades. Otras poblaciones, como L’Hospitalet, podrían responder especialmente a otros factores al ser la ciudad con mayor densidad de población de toda Europa.

Sin embargo, lo realmente importante es que el modelo permite recalibrar estas variables de idoneidad para adaptarse a distintos microorganismos. No todos se transmiten por el aire, ni responden igual a la bajada de temperaturas. Algunos patógenos se propagan a través de las aguas residuales y otros por vía sexual. Porque la meta de Liberthal y Gardner no es tan solo crear un modelo predictivo para la propagación de la COVID-19, sino uno suficientemente maleable para adaptarse a las pandemias que, sin duda, aún están por llegar.

QUE NO TE LA CUELEN:

• El modelo promete ser útil para todo tipo de enfermedades infecciosas, ya sean de transmisión directa, como es el caso del SARS-CoV-2, o bien de transmisión indirecta a través de insectos, por ejemplo, como es el caso de los mosquitos para la malaria. Hará falta calibrar y aplicar el modelo en otras poblaciones para seguir validando su utilidad predictiva.

REFERENCIAS:

• Lieberthal, Brandon, and Allison M. Gardner. “Connectivity, Reproduction Number, And Mobility Interact To Determine Communities’ Epidemiological Superspreader Potential In A Metapopulation Network”. PLOS Computational Biology, vol 17, no. 3, 2021, p. e1008674. Public Library Of Science (Plos), doi:10.1371/journal.pcbi.1008674. Accessed 20 Mar 2021.