El tuit viral que le saca los colores a ChatGPT

Imagínate que participas en un concurso de televisión en el que el presentador te muestra tres puertas. Detrás de una de ellas, te comenta, hay un coche, mientras que detrás de las otras dos hay cabras. Tú debes elegir una de las puertas y, cuando lo hagas, el presentador abrirá una distinta, mostrando una cabra. A continuación, el presentador te ofrece la posibilidad de cambiar de puerta o quedarte con la que elegiste. ¿Qué decides?

A lo mejor has pensado que da igual lo que hagas, siempre tendrás la misma probabilidad de ganar el coche. Al fin y al cabo, sabes a ciencia cierta que, de las dos puertas que siguen cerradas, una tiene un coche y la otra una cabra.

Sin embargo, te conviene mucho más cambiar de puerta, ya que, si lo haces, doblarás tu probabilidad de ganar el coche.Si esta conclusión no te parece intuitiva, estás en buena compañía: se trata del famoso Problema de Monty Hall, llamado así en honor al presentador de un concurso de televisión estadounidense que tenía una prueba parecida a esta, y ha sido objeto de muchísimo debate a lo largo de las décadas.

Pregúntale a Marilyn

Aunque el problema original, junto con su solución, lo propuso el estadístico Steve Selvin en 1975, la fama llegó gracias a Marilyn vos Savant en 1990. Cuando batió el récord Guinness al cociente intelectual (categoría que se acabó retirando del catálogo), vos Savant inauguró una columna titulada “Ask Marilyn” (“Pregúntale a Marilyn”) en la revista dominical Parade, donde respondía a preguntas de los lectores.

En una ocasión, la pregunta de un lector planteaba el Problema de Monty Hall, y vos Savant formuló la respuesta correcta. Sin embargo, miles de lectores le escribieron alegando que no estaban de acuerdo con su resolución. Muchos de ellos incluso presumían de tener un doctorado, pero no por ello repararon en que vos Savant tenía razón.

Nunca sabremos si las columnas adicionales que escribió vos Savant para explicar su razonamiento convencieron a sus lectores más fieles, pero sí podemos analizar las probabilidades de ganar en diferentes situaciones para, al menos, comprender por qué nos conviene cambiar la puerta elegida.

Por qué conviene cambiar

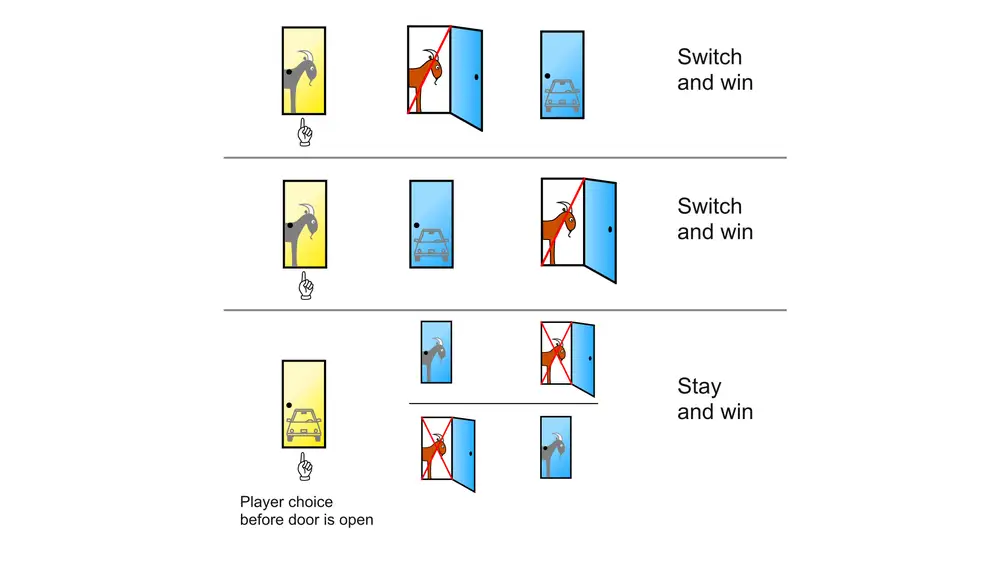
Al inicio del juego, sabes a ciencia cierta que, de las tres puertas, solo una tiene el coche. Por eso, la probabilidad de que aciertes, es decir, de que elijas la puerta que tiene el coche, es de un tercio. Por el mismo motivo, la probabilidad de que pierdas es de dos tercios. Es decir, si consideramos las otras dos puertas en conjunto, la probabilidad de que el coche esté detrás de ellas es de dos tercios.

Pongamos que elegiste la puerta número 1, y que el presentador abre la número 3 para mostrarte una cabra. Cuando el presentador abre la puerta 3, estas probabilidades no cambian: la puerta 1 sigue teniendo una probabilidad de un tercio de tener el coche. Lo que sucede ahora es que, de entre las puertas 2 y 3 (que, juntas, tienen una probabilidad de dos tercios, recordemos), tú ya sabes que la 3 no tiene el coche.

Por tanto, la puerta 2 es la que tiene el coche con una probabilidad de dos tercios: el doble que la puerta 1, que es la que elegiste inicialmente. Sin duda, te conviene cambiar tu apuesta.

Efectivamente, es necesario pararse a razonar muy cuidadosamente para convencerse de esta idea. Precisamente por eso, la psicología cognitiva sigue tratando de explicar por qué la mayoría de las personas, incluso aquellas muy formadas, llegan a una conclusión errónea.

El tuit viral

Tan estudiado está el problema que, si le explicamos las premisas a ChatGPT y le pedimos que nos recomiende una estrategia, no solo nos dirá claramente que debemos cambiar de puerta, sino que nos preparará todo un razonamiento lógico para explicarlo y nos advertirá además de que, a pesar de ser poco intuitiva, esa es la estrategia correcta.

Pero es más sorprendente aún su respuesta a una variante del problema tan simplificada que resulta cómica, y que se hizo viral en Twitter esta semana. La variante dice así:

“En un concurso, el presentador, Monty Hall, te muestra tres puertas. Primero abre cada una de las puertas para que veas que, detrás de la puerta 1, está el premio mejor: un coche de lujo, mientras que detrás de las puertas 2 y 3 hay cabras. También te asegura de que, según las reglas del juego, los premios no se pueden mover. A continuación, cierra las tres puertas y te pide que elijas una. Tú eliges la puerta 1, detrás de la cual —por enfatizar— está el coche: el premio que quieres más que ningún otro. Ahora, Monty abre la puerta 3, mostrándote una cabra. A ti no te sorprende porque ya habías visto que estaba ahí. Monty te ofrece la oportunidad de cambiar tu elección de la puerta 1 a la 2 a cambio de $100. Tú quieres el coche. ¿Cambias a la puerta 2 o te quedas con la puerta 1 donde está el coche?”

Esta versión no tiene ninguna complicación matemática: sabes de antemano dónde está el coche, eliges esa puerta y, claro está, no tiene sentido cambiar tu apuesta. Sin embargo, ChatGPT recomienda tajantemente: “Deberías cambiar a la puerta 2”. ¿Por qué?

Este es un buen ejemplo de que ChatGPT no es capaz de razonar como lo haría una persona, y cualquier otro generador de texto tampoco. Una prueba de ello es que, después de darnos el consejo equivocado y recomendar que cambiemos a la puerta 2, ofrece una profusa explicación, partiendo de que la probabilidad de que el coche esté detrás de la puerta 1 es de un tercio. Pero, en esta versión simplificada del problema, tenemos la certeza absoluta de que el coche está detrás de la puerta 1, así que no es necesario ni siquiera comenzar a razonar con probabilidades.

Si ChatGPT se empeña en remitir a la solución del problema original es porque ha aprendido a partir de una base de datos gigante, procedente de textos encontrados en internet, en la que figura el Problema de Monty Hall original, con su solución poco intuitiva y múltiples explicaciones de por qué, a pesar de todo, es la correcta. Sin embargo, en la base de datos no hay apenas variantes como la que tenemos entre manos, ya que no estan frecuente que se hable de ellas en internet.

El programa, entonces, ofrece una respuesta que tiene una probabilidad alta de ser correcta dados los textos de la base de datos de entrenamiento, y, al menos a día de hoy, no es capaz de detectar si está ante un caso que para una persona humana es muchísimo más sencillo que el habitual.

Es probable que las futuras versiones de ChatGPT mejoren en su capacidad de responder ante situaciones como esta, aunque siempre será un modelo probabilístico no dotado de sentido común. Pero, para que una herramientatan potente como ChatGPT nos sea realmente útil a los humanos, es crucial comprender muy bien sus límites.

QUE NO TE LA CUELEN:

• Ni siquiera hace falta llegar a la complejidad del Problema de Monty Hall para que ChatGPT se tropiece. Otro tuit del mismo hilo proponía: “¿Qué pesa más, un kilo de plumas o 2 kilos de ladrillos?” y ChatGPT contestaba que “Tanto un kilo de plumas como 2 kilos de ladrillos pesan lo mismo, es decir, un kilo”.

REFERENCIAS (MLA)

• Selvin,Steve. “Letters to the Editor.” The American Statistician, vol. 29, no.1, 1975, pp. 67–71., https://doi.org/10.1080/00031305.1975.10479121.
• “GameShow Problem.” Marilyn Vos Savant, https://web.archive.org/web/20130121183432/http://marilynvossavant.com/game-show-problem/.
• LeCun, Yann, et al. “Deep Learning.” Nature, vol.521, no. 7553, 2015, pp. 436–444., https://doi.org/10.1038/nature14539.