
Medicina
A nadie le interesa la forma de sus células (hasta que dices ESCUTOIDES)
Hace un par de años la forma de nuestras células se convirtió en un icono pop gracias a los escutoides, pero ¿por qué?

Es fácil olvidarnos de quiénes somos. Recordamos nuestro nombre, nuestro pasado e incluso esa canción pegadiza que estuvo de moda hace años, pero olvidamos algo fundamental: que no somos uno, somos legión. Somos una comunidad de células que trabajan juntas, como un todo. A efectos prácticos, esto no supone una gran diferencia para nuestras actividades cotidianas, compraremos el pan del mismo modo y seguiremos tomando el bus igual que siempre. Sin embargo, para la medicina la historia fue muy distinta. Nada volvió a ser lo mismo tras descubrir que ese continuum de carne, huesos y vísceras no era tan continuo, sino que estaba formado por pequeñas unidades básicas, células colocadas como bloques de construcción.
Escucha"2. La extraña forma de tus células. Luisma Escudero" en Spreaker.Podemos decir, por lo tanto, que la sociedad como conjunto y los científicos como colectivo no encuentran interesantes los mismos detalles. Dicho de otro modo, es fácil atrapar al público hablando sobre agujeros negros o nuevos materiales como el grafeno, pero cuando hablamos de células la historia cambia. Incluso cuando se trata de un descubrimiento realmente crucial y revolucionario, el mundo celular no consigue abrirse paso hasta las calles. Sin embargo, hace ya 2 años sucedió algo inesperado. Un artículo escrito por un equipo liderado por el doctor Luisma Escudero de la Universidad de Sevilla, se extendió más rápido que cualquier pandemia. El descubrimiento cruzó el océano y viajó de televisión en televisión hasta acabar en boca de todo el mundo. De un Nature Communications, terminó llegando al monólogo en Prime Time de Stephen Colbert, el presentador de Late Shows más famoso de todo Estados Unidos (y posiblemente del mundo).
Pero ¿qué célula?
Tal vez, lo primero que haya que entender es que no todas nuestras células son iguales. Su forma varía mucho más de lo que pensamos. Es posible que conozcas la forma de las neuronas, esas células de nuestro cerebro con aspecto de árbol, extendiendo desde sus cuerpos dendritas a modo de ramas, y un largo axón que recuerda al tronco. Sin duda, estas no se parecen en nada a los miocardiocitos de tu corazón, que recuerdan más a los puntos de un grueso jersey de lana, enredándose entre ellos para formar una malla capaz de estirarse y contraerse. El caso es que ni siquiera esto representa la verdadera diversidad ante la que nos encontramos, porque esa neurona que imaginas no existe.
O mejor dicho, es como el ideal abstracta de neurona, de la cual se separan notablemente sus versiones del mundo de los sentidos. Estas pueden no tener más que una dendrita muy larga, casi como si fuera otro axón, otras de estas ramas, pueden salir directamente del tronco, haciendo que del cuerpo neuronal solo parta una prolongación. Así de compleja es la diversidad morfológica de nuestras células. En parte tiene todo el sentido del mundo, ya que en biología, estructura y función van de la mano y si una neurona tiene tal o cual forma, posiblemente se deba a que esa es la estructura que mejor cumple con su cometido (dentro de un margen, claro).

El problema es que las neuronas no son representativas de lo que conocemos o dejamos de conocer sobre la forma de las células. Cuando hablamos de la función de las células que, a grandes rasgos, hacen posible nuestro intelecto, es normal tratarlas con una reverencia excesiva y prestar especial atención a su estructura en busca del origen a tan compleja función. No obstante, cuando hablamos de nuestra piel la cosa cambia. Quien dice piel dice mucosa intestinal o glándulas, en definitiva, células epiteliales, aquellas que recubren nuestro exterior y nuestro interior. Incluso los científicos, sabiendo sus importantes y complejas funciones, tendemos a verlas como poco más que bloques apilados por capas, y, de hecho, así los representamos en libros de texto y artículos.
Ni esferas ni prismas ni estructura de Weaire-Phelan
Hasta cierto punto parece incluso lógico. Pensemos que apilar esferas no es lo más fácil del mundo, y si no imaginemos esas pirámides de naranjas de los supermercados. Las células se unen unas a otras, adhiriendo aquellas superficies que están en contacto. Así pues, cuanto más contacto más posible será que establezcan estructuras de unión y que el tejido esté más cohesionado. Entonces, ¿cuál la mejor forma geométrica para que, al unir muchos bloques iguales, quede una estructura bien compacta?
Desde la Grecia clásica se ha tratado de resolver este tipo de cuestiones. Papo de Alejandría (Pappus) demostró que la figura geométrica regular que mejor cubría una superficie era el hexágono. El problema es que el mundo real no tiene dos dimensiones. Todo tiene cierta profundidad, por pequeña que sea, e hicieron falta muchos siglos hasta que en 1993 se demostró que la mejor figura tridimensional para cubrir un espacio era la estructura de Weaire-Phelan.
El problema es que no estamos ante un problema de matemática teórica que pueda olvidarse de las limitaciones que hay en el mundo real. Limitaciones como la forma final del tejido a crear, sus curvas y las propiedades mecánicas de las células que lo componen. Por eso, la aproximación tradicional de los biólogos ha sido mucho más intuitiva, independientemente de su validez.
Las paredes de nuestros edificios están hechas de ladrillos, y los cartones de leche se amontonan a la perfección. Son prismas, esto es: figuras tridimensionales formadas por dos caras paralelas unidas por paralelogramos (más caras cuyos lados son paralelos dos a dos, como un rectángulo o un rombo). En el caso de los ladrillos, las caras paralelas, la base y la parte de arriba, son rectángulos, pero puede tratarse de cualquier otra figura. Por ejemplo, podemos poner dos hexágonos uno sobre el otro a cierta distancia, y unir sus seis esquinas con cada una de las del otro hexágono, formando una columna cuyo contorno está definido por seis lados, en lugar de los cuatro que tornean al ladrillo. Entonces ¿ya estaría?
Para ser sinceros, de la biología no es esperable un prisma perfecto, sino otro tipo de prismatoide, como el frustum. En ellos, su base y su parte de arriba no tienen por qué tener el mismo tamaño, por lo que tampoco tienen por qué estar unidos por paralelogramos, sino que pueden ser, por ejemplo, trapezoides. Podemos compararlo con una pirámide cortada a media altura, “truncada” que se dice en geometría. Esta forma de frustum era bastante interesante, porque permitía algo que los cartones de leche, los prismas, no son capaces de hacer, y es crear superficies curvas. Porque nuestra piel no es una capa plana de tejido, nos recubre adaptándose a los relieves de nuestra anatomía. Y, por si fuera poco, nuestro intestino por dentro no es solo un tubo, sino que dicha cavidad tiene una enorme cantidad de pequeños pliegues que aumentan su superficie para facilitar la absorción de nutrientes.

No obstante, había un pequeño problema, y es que, a pesar de que la comunidad científica había aceptado la forma de frustum casi sin cuestionarla, esta no podía explicar algunas cosas que ocurren en el mundo real. Y aunque algunos teóricos sufran una reacción anafiláctica al escuchar esto: cuando tu modelo teórico no sea justo a lo que observamos en la realidad, casi seguro que el problema sea de la teoría. Pero ¿cuál era ese problema?
Une los puntos
A pesar de las discrepancias que hemos dicho, había algo que sí estaba bastante aceptado por la comunidad. Y es que cuando vemos solo la superficie de un tejido, sus células se disponen siguiendo la estructura de un diagrama de Voronoi. Si alguna vez has intentado hacer galletas sabrás a lo que me refiero. Cuando las colocas en la bandeja son pequeñas, pero durante el horneado se expanden. Si no las has puesto suficientemente lejos unas de otras, al crecer, pueden llegar a colisionar. Pues bien, la zona donde se encuentran forma una frontera en línea recta. Si cada galleta antes de hornear fuera un punto, esas líneas de colisión estarían exactamente en el medio, a igual distancia de ambos puntos originales. Esto significa que, cuando hay muchas de estas galletas-puntos (semillas, que llaman los matemáticos), las líneas se encontrarán entre sí formando el contorno de polígonos, formas geométricas con más o menos lados. La gracia es que, cada uno de esos hexágonos, o pentágonos que se formen, cumple la característica de que, cualquier punto que se encuentre dentro de él (de su área de influencia) estará más cerca de la semilla de esa área que de ninguna otra.

Gracias a esto tu teléfono puede indicarte dónde está la farmacia más cercana, por ejemplo. Lo mismo ocurre cuando dos pompas de jabón se tocan, y por supuesto, cuando varias células entran en contacto. Si la idea del frustum fuera cierta, tejidos formados por una sola célula de grosor deberían tener diagramas de Voronoi muy parecidos ente sus dos superficies. Dicho de otro modo: una célula en un lado de ese tejido tendría que estar rodeada exactamente por las mismas células que están en contacto desde el otro lado del tejido. Pero eso no fue lo que vio el equipo del doctor escudero cuando trató de simular estas células en la superficie curva de un tubo. Algunas células que se tocaban en un lado de la capa, en el otro estaban separadas, y no eran pocas las que se encontraban en esta extraña situación.
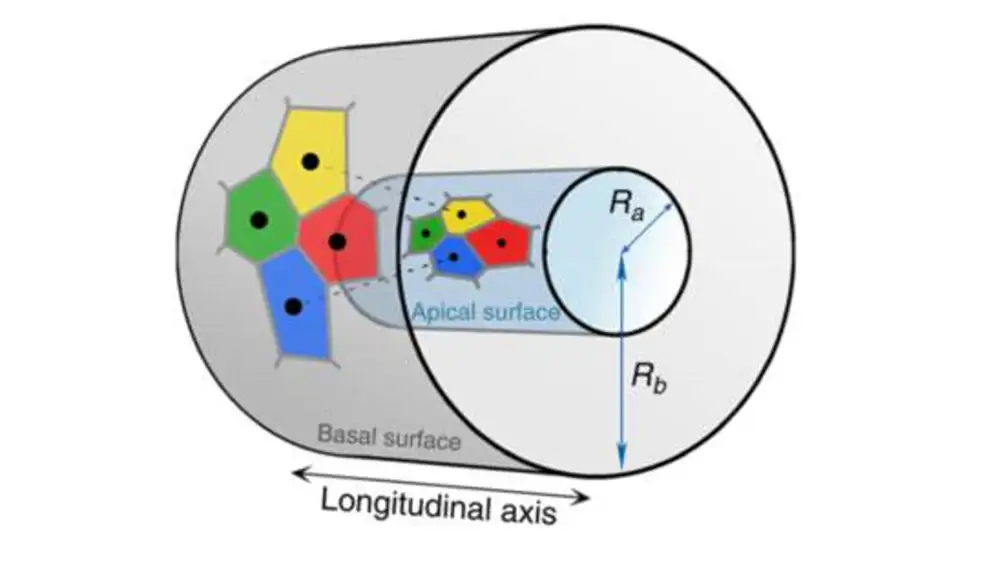
Entonces, ¿a qué se debía este extraño fenómeno? Los investigadores ya tenían claro que, una célula podía mostrar una base hexagonal por un lado y un pentágono por el otro, implicando pequeñas diferencias, había prismatoides que explicaban esa discrepancia uniendo uno de los vértices del pentágono con dos del hexágono, por ejemplo, pero nada de eso explicaba que una célula cambiara a sus vecinas. La respuesta estaba, precisamente, en los escutoides.
Escutoides
Normalmente se representa al escutoide como un prismatoide formado por un hexágono unido a un pentágono, pero que, en lugar de unir los vértices sobrantes del hexágono al mismo vértice del pentágono con una especie de “V”, lo hacen con una “Y”, pero esto es tan solo el ejemplo que se ha popularizado, un caso particular. Los diagramas de Voronoi no siempre forman pentágonos o hexágonos, aunque estos son relativamente frecuentes en estas superficies tisulares. Lo importante no es tanto el número de lados del escutoide, sino el hecho de que esa “Y” le proporciona, al menos, un vértice extra en su contorno, más allá de los de su base y su parte de arriba. Eso y sus superficies, que en lugar de completamente rectas tienen cierta curvatura, eran la clave para explicar cómo, pudiendo unirse a la perfección unos con otros, pueden trazar fronteras con células diferentes en cada uno de los lados de una misma capa.

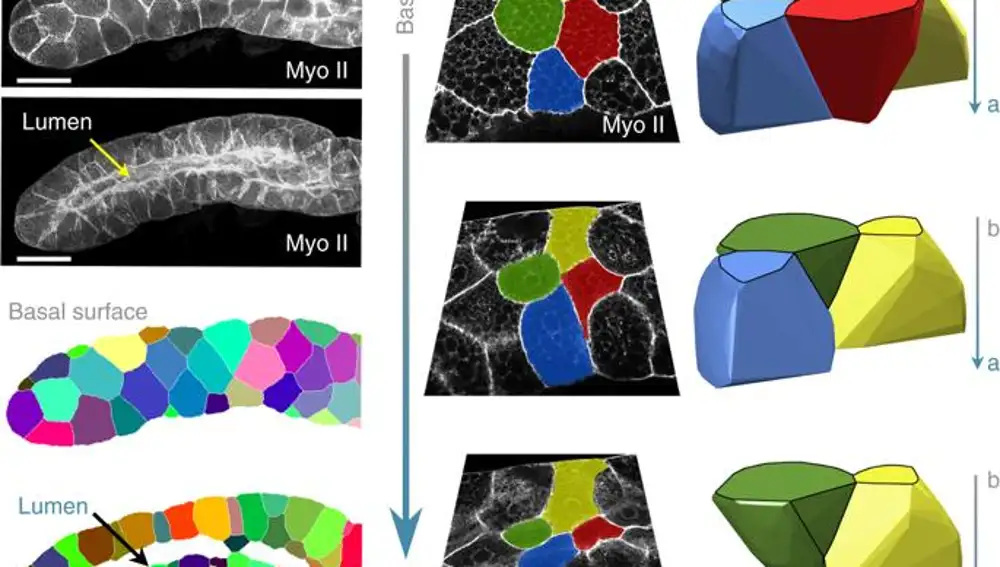
Al menos esto era hacia donde apuntaba el modelo matemático, pero como pudo comprobar el equipo del doctor Escudero, estas mismas estructuras (aunque algo menos definidas, por supuesto) estaban presentes en las glándulas salivares de las moscas.
Y si con esto fuera poco, el propio artículo que saltó a la fama analiza las propiedades físicas del escutoide explicando su aparente complejidad geométrica y demostrando que su estructura es especialmente económica energéticamente hablando. Dicho con otras palabras: el escutoide no solo permite crear superficies curvas, sino que es ideal para conseguirlo gastando la menor cantidad de energía posible, lo cual es, precisamente, lo que esperaríamos que la selección natural hubiera potenciado durante la evolución.
La pregunta impertinente
El escutoide era real, tenía un nombre pegadizo, podía visualizarse y era bastante mono. ¿Fue esto lo que causó furor? Puede que en parte sí, pero ¿qué implicaciones tiene? Una pregunta así es casi una impertinencia en ciencia básica, pero para contentar a lectores pragmáticos diremos que, entender la forma de nuestras células epiteliales nos permitirá diagnosticar mejor las enfermedades en las que pueda verse alteradas. Normalmente se ejemplifica nombrando a los temidos procesos tumorales, donde un grupo de células se reproduce sin control y se “suelta” de sus vecinas cambiando la estructura del tejido donde se encuentra.
Es más, podemos decir que si entendemos bien las propiedades de esta estructura podremos profundizar con mayor facilidad en las grandes preguntas de la biología del desarrollo. ¿Cómo se organizan las células en los tejidos que terminarán formando nuestros órganos? ¿Por qué a veces fallan? Son cuestiones secundarias que, una vez resueltas, nos permitirían avanzar en la creación de organoides y órganos artificiales, retroalimentando una vez más la carrera de relevos que es la investigación científica.
Aquella investigación se convirtió en un fenómeno de masas sin precedentes en el mundo de la ciencia a pequeña escala, pero ¿por qué? Sin duda era un tema interesante para la comunidad científica y ponía fin al paradigma imperante hasta aquel momento. Su multidisciplinaridad aunando a biólogos, matemáticos, informáticos y físicos dio lugar a un artículo precioso, pero ¿tanto? A diario se publican una infinidad de investigaciones y algunas de ellas son revolucionarias en sus campos. Son muchos los descubrimientos que cada año suponen una pequeña revolución en sus disciplinas y algunos incluso tienen la suerte de cambiarlas a lo grande. ¿Por qué no consiguen ni siquiera la mitad de impacto?
Nada de esto es una crítica, todo lo contrario. Es un halago al magnífico trabajo de popularización que han hecho los investigadores. Y aunque parte del éxito siempre se debe a factores que no están en nuestras manos, siempre podemos intentar aprender de ellos y de cómo consiguieron que un tema que no interesa a nadie salvo a los propios científicos, se convirtiera en la canción del verano de 2018.
Escucha"2. La extraña forma de tus células. Luisma Escudero" en Spreaker.QUE NO TE LA CUELEN:
- No todas las células epiteliales son como la imagen popularizada de los escutoides, ni se ha demostrado que otros tipos de células tengan esta estructura.
REFERENCIAS (MLA):
✕
Accede a tu cuenta para comentar


