Matemáticas
Números trascendentes y dónde encontrarlos
Los números trascendentes son el dragón que se esconde en el océano de los números. Y cuando miramos de cerca vemos que hay más dragones que agua.
Los números son, sin duda, los habitantes más conocidos del mundo de las matemáticas. Los usamos todos los días para dar la hora, o para decir cuánto vale la compra. Decimos con toda naturalidad “ese coche medirá unos cuatro metros”, y somos conscientes de que si tuviéramos un metro podríamos afinar más y decir que mide 4,12 metros. Incluso con algún aparato de medida realmente bueno podríamos ir al detalle fino, y decir que entre estos dos puntos hay exactamente 4,11875 metros. Los números parecen un pozo sin fondo: siempre podemos seguir añadiendo dígitos, y parece que el único límite son nuestros aparatos de medida y nuestra paciencia. Pero en ese océano de los dígitos se esconden dragones, y a esos seres es a los que vamos a visitar hoy.
Números decimales
En nuestra vida diaria rara vez usamos números con más de tres cifras decimales. Si unas galletas valen dos euros y sesenta céntimos su precio es de 2,6 euros; si una tabla de madera mide un metro y trece milímetros su longitud es 1,013 metros. Estos números tienen una interpretación muy sencilla: 2,6 euros significa “dos euros + seis décimas de euro”, o también “260 céntimos de euro”. 1,013 metros es, por ejemplo, “1013 milímetros”. Todos los números que tienen una cantidad finita de decimales son equivalentes a “cierta cantidad de alguna cosa”. Esto es cierto incluso para los números con muchos decimales, que no solemos usar tan a menudo. Por ejemplo, “0,000032 segundos” es lo mismo que “32 millonésimas de segundo” o, en jerga de físicos, 32 microsegundos.
Los números con una cantidad finita de decimales, pues, no tienen secreto. Pero luego existen esos números tan molestos cuyos decimales siguen y siguen hasta el infinito. Por ejemplo, 0,3333…; o π, que vale 3,1415927… Estos números ya no podemos entenderlos como “una cantidad finita de algo”, porque la ristra de dígitos no termina nunca, y por lo tanto no podemos fijar cuánto vale esa cantidad. Estamos ante el océano de los números, un lugar en el que es fácil perderse si no se tiene un buen mapa.
Fracciones y raíces
Algunos de los números del océano sabemos interpretarlos. Por ejemplo, 0,333… sabemos que es una fracción: el número ⅓. Esto nos devuelve a un terreno cómodo, porque “un tercio” vuelve a ser una cantidad finita de alguna cosa; en concreto, “divida esto en tres partes y déme una”. De hecho, hay una regla útil: las fracciones o bien tienen un número finito de decimales o bien, si es infinito, es una secuencia que se repite. Por ejemplo, ⅕ es 0,2, o 1/11 es 0,090909… Y por fortuna para nosotros lo contrario también es cierto: cualquier ristra infinita de decimales con una secuencia que se repite es una fracción. Así que cuando veamos algo muy desagradable como 0,142857142857… no hemos de temer: hacemos un poco de álgebra y descubrimos que es 1/7. Todo en orden.
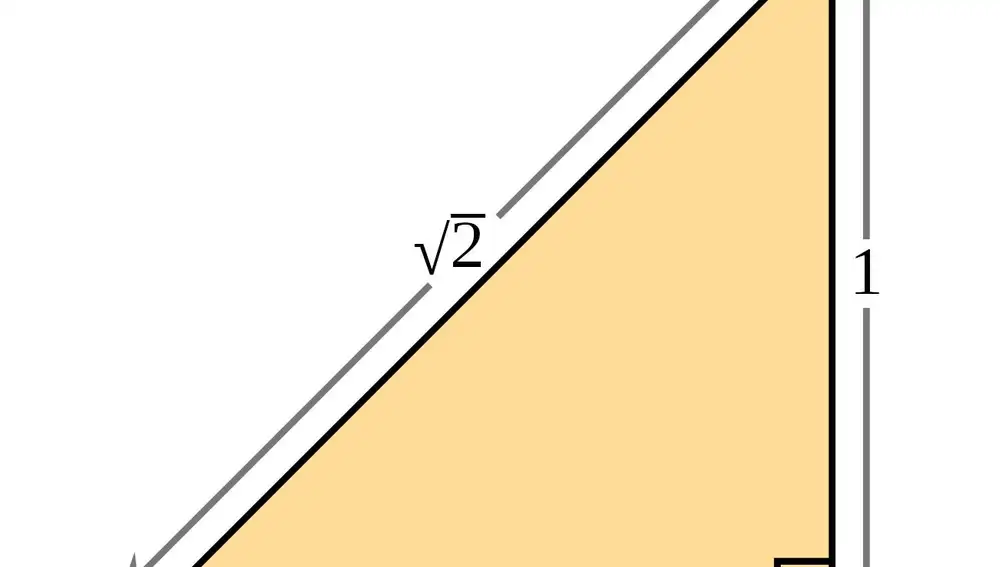
Las fracciones son el animal más dócil de este océano de los números. El siguiente son las raíces. Todos hemos sufrido un poco calculando raíces cuadradas a mano con arcanos algoritmos olvidados, y hemos dado las gracias a los dioses del silicio por que existan los ordenadores y otros ingenios eléctricos que nos hacen la vida más fácil. A lo que iba: que la mayoría de las raíces tienen expresiones decimales infinitas, y éstas no son como las de las fracciones, que las podemos reconocer porque hay una secuencia que se repite. Un ejemplo típico es √2, que vale 1,4142135… ¿Quiere esto decir que estamos condenados a perdernos en un mar de raíces con infinitos decimales?
Por fortuna, las raíces tienen una cosa en común: todas son soluciones de una ecuación polinómica. Por ejemplo, √2 es la solución de x² - 2 = 0, o ∛5 es la solución de x³ - 5 = 0. De hecho, cualquier combinación de raíces y fracciones que se nos ocurra es la solución de una de estas ecuaciones con todos sus coeficientes enteros. Éste es un tipo de ecuación especialmente sencilla: consiste en un número, más un número por x, más un número por x², más un número por x³, y así sucesivamente. Esto quiere decir que, si queremos, podemos sustituir en nuestra cabeza la expresión decimal de la raíz, con sus infinitas cifras, por la ecuación que le corresponde, mucho más manejable y perfectamente finita. Hemos encontrado una nueva forma de “dar nombre” a los números: mediante las ecuaciones de las que son solución.
Esta idea es de muy largo alcance. A los números que son solución de una ecuación polinómica con coeficientes enteros los llamamos en general números algebraicos. Son algebraicas las raíces, pero también lo son todas las fracciones y todos los números enteros. Más importante todavía: también son algebraicos un buen puñado de números en los que ni siquiera se nos había ocurrido pensar hasta ahora. Por ejemplo, la ecuación x^5 - x - 1 = 0 tiene una solución en los números reales, localizada en x=1,1673… Esta solución no se puede expresar con fracciones, y por lo tanto tiene infinitos decimales sin ninguna secuencia que se repita. Pero es que tampoco puede expresarse con raíces. Es, simplemente, un número algebraico: la solución de x^5 - x - 1 = 0. Como este número hay muchos otros, todos solución de ecuaciones de grado 5 o superior. Estos números necesitan las ecuaciones para tener nombre, porque sus infinitos decimales no caben en ninguna página.
El océano trascendente
La siguiente pregunta es muy predecible: ¿dan cuenta los números algebraicos de todos esos números con infinitas cifras decimales que no son fracciones? La respuesta es no. Y es un gran no, porque es posible demostrar que los números algebraicos son sólo una minúscula minoría dentro del gran océano de los números. La mayor parte tienen infinitos decimales y no están asociados a ninguna ecuación polinómica. Los llamamos números trascendentes porque van más allá del simple cálculo algebraico, que sólo usa polinomios, divisiones y raíces.
Los números trascendentes son el más extraño de los animales numéricos. Aparecen relacionados con funciones no polinómicas, como la exponencial y el coseno, pero también emergen en algunas propiedades aparentemente sencillas de los objetos matemáticos. Por ejemplo, la relación entre la longitud de una circunferencia y su diámetro es un número trascendente. Ese número, claro, se llama π, y todo el mundo lo conoce. Las matemáticas, en cierta manera, nos están diciendo que no todas las cosas importantes se construyen sobre números sencillos, o quizá que algunos objetos matemáticos tienen su propio lenguaje y necesitan sus propios números.
Clases de trascendencia
Es difícil hacer afirmaciones generales sobre los números trascendentes. Al fin y al cabo, los definimos por oposición: son un cajón en el que metemos todo lo que no conseguimos explicar con polinomios; es lógico pensar que formen un magma relativamente inhomogéneo, en el cabe casi cualquier cosa, desde piedras angulares de la geometría como π a números más o menos caprichosos como el 0,1020030004…
Pese a todo, sí disponemos de una clasificación de brocha gorda de los números trascendentes. La desarrolló el matemático alemán Kurt Mahler en la década de 1930, y se basa en cómo de bien podemos aproximar un número trascendente usando números algebraicos. La idea es la siguiente: como los números trascendentes no son solución de ecuaciones polinómicas, yo puedo coger cualquier polinomio y sustituir su variable por un número trascendente y eso nunca me va a dar cero. Pero ¿cuánto puedo acercarme al cero? ¿Hay números trascendentes que casi consiguen resolver una ecuación polinómica?
La respuesta es que sí. Mahler descubrió que hay tres clases de números trascendentes: la más “cercana” a los números algebraicos es la clase U. Los números U no hacen cero ninguna ecuación polinómica, desde luego, pero para un grado suficientemente alto yo siempre puedo encontrar polinomios de forma que al sustituir el número U el resultado sea tan próximo a cero como quiera. El grado es el exponente máximo del polinomio, y cuanto más alto es el grado más complicado es el polinomio, así que tiene sentido empezar con los grados más bajos. Un número es de clase U si no consigue acercar a cero ningún polinomio de grado n, pero al probar con los de grado n+1 resulta que puedo ajustar los coeficientes de forma que el resultado sea tan pequeño como yo quiera. Un número U, pues, es “casi un número algebraico de grado n+1”.
La siguiente clase es la clase T. Los números T no consiguen acercar a cero ningún polinomio de grado fijado, pero si me permito aumentar el grado tanto como necesite sí que podré disminuir el valor del polinomio tanto como quiera. Los números T son “casi un número algebraico de grado infinito”.
La clase final es la clase S. Éstos son los números trascendentes pata negra. Con éstos ni aumentando el grado ni cambiando los coeficientes logro que los polinomios bajen de un cierto valor. Los clase S no se parecen a un número algebraico y no quieren parecerse; pasan totalmente de los polinomios. Lo que viene a continuación quizá no sea una sorpresa: la abrumadora mayoría de números trascendentes, y por tanto la mayoría de números, son números S.
Este resultado, que es un pelín frustrante, en realidad también tiene cierto sentido: ¿por qué iban las matemáticas a preferir los polinomios? ¿Por qué iban a estar la mayoría de los números relacionados con un tipo de función muy concreta y muy restringida? Las matemáticas nos dicen que no. Que ellas hacen sus propias reglas, que los números son su territorio. Nosotros somos, a lo sumo, un escribano o un cartógrafo, tratando de trazar un mapa para orientarnos en este océano de dragones.
QUE NO TE LA CUELEN
- En este artículo nos hemos limitado a hablar de números reales, que no son ni mucho menos los únicos que hay. Existen números algebraicos que no son reales ‒los números complejos, por ejemplo‒ y existen números que son alternativas a los reales.
- La palabra “trascendente” aplicada a los números no tiene ningún tipo de connotación mística. Al contrario, lo que refleja es la sorpresa de los matemáticos de los siglos XVII y XVIII al descubrir que algunos números superaban el marco de las ecuaciones algebraicas.
REFERENCIAS
- Edward Burger y Robert Tubbs. Making transcendence transparent. An intuitive approach to classical transcendental number theory. Springer (2004)
✕
Accede a tu cuenta para comentar


