Números p-ádicos, cuando “cerca” pasa a ser “lejos”

Los números son abstracciones. No existe un objeto llamado “número tres”, sino que llamamos “tres” a eso que tienen en común todos los grupos de tres cosas, independientemente de que esas cosas sean manzanas, sillas o granos de arroz. Los números, por su propia naturaleza, nos piden que vayamos un poco más allá del mundo que vemos con nuestros ojos: son seres abstractos y, en cierta manera, sólo existen en nuestra cabeza. Por eso, para poner a prueba la inteligencia de los animales, es habitual tratar de averiguar si conocen la noción de número.

Todos los números son abstractos, eso está bien. Pero algunos son sin duda más abstractos que otros. Hoy vamos a hacer un recorrido por las entrañas de los números para acercarnos a un tipo de número muy desconocido y algo exótico: los números p-ádicos, que nacen de cambiar nuestra noción de “cerca” y “lejos”.

El mundo de las fracciones

Los números más sencillos son los números naturales: el uno, el dos, el tres… éstos los entendemos todos de forma más o menos intuitiva. Con los números naturales sabemos sumar y multiplicar, y el resultado siempre es otro número natural. Cuando los queremos restar o dividir, en cambio, los naturales se nos quedan cortos: si quiero hacer la resta 5-10, por ejemplo, necesitaré un número que esté por debajo del cero. Para eso inventamos los números negativos.

Pero hoy nos va a interesar más la división. Cuando dividimos números naturales obtenemos las fracciones, como ½ o ⅗. Las fracciones tienen una propiedad interesante, que los números naturales no tienen: pueden estar muy cerca unas de otras. Lo más cerca que dos números naturales pueden estar es a 1 unidad: el 2 y el 3, por ejemplo, o el 27 y el 28. En cambio, las fracciones pueden estar muy cerca: entre ½ y ⅓ hay ⅙ de unidad, y si nos empeñamos podemos encontrar fracciones que estén todo lo cerca que queramos. Entre ½ y ⅗, por ejemplo, hay sólo 1/10 de unidad.

Esta última propiedad es interesante, porque tiene consecuencias bastante espectaculares. Si puedo encontrar fracciones tan cercanas como quiera… ¿cuántas fracciones hay entre 0 y ½? Bueno, tenemos ¼, claramente. Y entre ¼ y 0 está ⅛. Y entre ⅛ y ¼, 3/16. Y eso por no hablar de ⅓, 1/9, y ⅕… Esencialmente, entre dos fracciones cualesquiera puedo encontrar tantas fracciones como quiera. Hay infinitas fracciones entre 0 y 1, infinitas entre 0 y ¼, infinitas entre ½ y ¾… las fracciones inundan el espacio entre los números, aparecen como setas y no nos podemos librar de ellas.

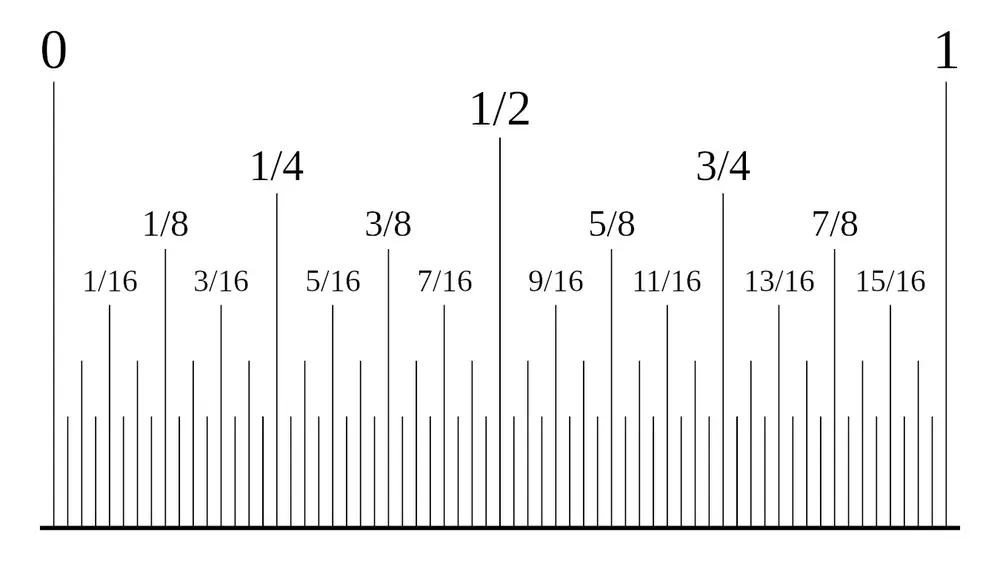
¿Significa esto que las fracciones llenan todo el espacio entre los números? No. Hay números entre 0 y 1 que no son fracciones. Es fácil verlo si escribimos las fracciones como números decimales. La fracción ⅕, por ejemplo, es el número 0.2, y la fracción ¼, el 0.25. La fracción ⅓ es el número 0.3333… (con una ristra de treses que nunca termina), y 1/11 es 0,09090909… (ahora la ristra es de los dígitos “09”). Todas las fracciones tienen una de estas dos formas: o bien un número decimal “que se termina”, como el 0.25, o un número cuyas cifras se repiten hasta el infinito, como el 0,090909… Esto da cuenta de todos los números que vamos a usar en nuestra vida diaria, porque normalmente vamos a querer números “de los que se terminan”: con dos cifras decimales, o quizá con tres, pero no mucho más. Todos esos números van a ser fracciones.

Números reales

Pero que no los usemos no quiere decir que no haya otros números. ¿Qué pasa con los números con infinitas cifras, pero que no se repiten? Un ejemplo sería el 0,12345678910111213… Es cierto que seguramente nunca haremos la compra con él, pero es un número y tiene sus derechos, así que vamos a tratar de entenderlo. Empecemos preguntándonos qué quiere decir que un número tenga infinitos decimales.

Una forma práctica de visualizar estos números es a través de secuencias formadas por números más fáciles de entender. Por ejemplo, consideremos la secuencia {0.3, 0.33, 0.333, 0.3333, ...}. Esta secuencia nos marca un “camino” que nos va llevando a un número que conocemos bien: el ⅓. Esencialmente, lo que nos dice es “Existe un número, el resultado de dividir 1 entre 3. La notación decimal no es muy apropiada para este número y resulta que ningún grupo finito de cifras lo puede representar. Pero si sigues este camino, el camino que marca esta secuencia, allá, al final, está el ⅓”.

Desde luego nadie puede seguir ese camino hasta el final, porque es un camino infinito y nuestra vida es finita. Pero sí podemos entender que ese camino tiene un final, porque cada paso es más pequeño que el anterior. En el primer paso avanzamos 0.3 unidades; en el segundo 0.03, porque 0.33 = 0.3 + 0.03; en el tercero avanzamos sólo 0.003; en el cuarto 0.0003… Claramente nos vamos acercando cada vez más a algo. Ese algo es el ⅓.

Pero ¿ocurre lo mismo con cada secuencia que podamos imaginar? No necesariamente. La secuencia {0.1, 0.12, 0.123, 0.1234, …} con la indicación de “las cifras sucesivas van recorriendo todos los números naturales” no termina en una fracción. Esa secuencia converge, está cada vez más cerca de alguna cosa, pero esa cosa no existe en el mundo de las fracciones. Es como si el conjunto de las fracciones tuviera “agujeros”. Llamamos números reales a los números que rellenan esos agujeros. El 0,12345678910111213… es uno de ellos.

Como vemos, esta noción de número nos está pidiendo un nivel de abstracción un poco superior: ya no se trata de números que sirven para contar, ni de números que sirven para hacer divisiones. Ahora estamos hablando de que no queremos que haya huecos entre nuestros números, que queremos poder pasar de un número a otro de forma continua, sin tener que saltar. Esta noción se llama compleción métrica, y los reales son los que completan métricamente a las fracciones, rellenando sus huecos.

Esta noción, sin embargo, tiene una sutileza en la que no solemos reparar: requiere del concepto de “cercano”. Imaginemos la secuencia {5, 10, 15, 20, …}. Esta secuencia no tiene a ningún número al final, y a nadie le extraña. En lenguaje matemático diríamos que la secuencia “tiende a infinito” y su final no lo vemos con los mismos ojos que el 0,3333… El infinito, en definitiva, no es un número. El ⅓ sí, y el 0,12345678910111213… también. ¿A qué se debe esto?

La razón es muy sencilla: las secuencias del 0,3333… y el 0,12345678910111213… están cada vez más cerca de algo, mientras que {5, 10, 15, 20, …} está siempre igual de lejos del infinito. Las secuencias de los números convergen; las del infinito, no. Esos “huecos” que vemos entre las fracciones están ligados a que sabemos medir distancias, y en base a eso decidimos qué secuencias convergen y cuáles se van al infinito. La pregunta es… ¿hay acaso más de una forma de medir distancias?

Métricas diferentes miden propiedades diferentes

Y la respuesta, claro, es que sí. En 1916 el matemático ruso Alexander Ostrowski demostró que si uno quiere medir la distancia entre dos fracciones tiene infinitas formas diferentes de hacerlo. La que conocemos y utilizamos habitualmente es una de ellas, y curiosamente es “la rara”, la que es un poco diferente. El resto tienen algunas características comunes y se llaman métricas p-ádicas (pronunciado “peádicas”).

Veamos cómo funcionan. El objetivo va a ser calcular la distancia entre dos fracciones, a y b. Con la métrica de toda la vida, la distancia va a ser b-a. Por ejemplo, la distancia entre 1 y 5 es simplemente 4. Las métricas p-ádicas van a coger este número y lo van a interpretar de forma… un poco diferente. En primer lugar, hemos de escoger un número primo, p. Las diferentes métricas p-ádicas sólo se diferencian en este número. Hecho esto, el quid de la cuestión va a ser si b-a contiene alguna potencia de p. Si b-a tiene potencias positivas de p, entonces b y a estarán cerca. Si b-a contiene potencias negativas de p, b y a estarán lejos. Finalmente, si no hay potencias de p en b-a, la distancia entre b y a será 1.

Vamos a verlo con unos cuantos ejemplos, para tratar de entender de qué va esto. Tomemos, por ejemplo, p=3, la métrica triádica. ¿Cuál será la distancia entre 1 y 5, que con la métrica habitual vale 4? Bueno, pues como 4=2×2 no tenemos potencias de tres, así que la distancia triádica entre 1 y 5 es… 1. Sin duda, diferente a lo que solemos utilizar. Veamos otro ejemplo: la distancia entre 1 y 6. Tenemos que 6-1=5, que no tiene potencias de tres. La distancia triádica entre 1 y 6 vuelve a ser 1. Lo mismo nos va a pasar con 2 y con 3: ambos están a una unidad triádica del número 1. Ya empezamos a imaginar que si tuviéramos que dibujar los números de acuerdo a esta distancia el resultado sería muy diferente a lo que conocemos.

Pero continuemos con algún otro ejemplo: ¿qué pasa entre 1 y 4? Ahora sí que tenemos 4-1=3, y es una potencia positiva de tres. Eso quiere decir que esos dos números van a estar cerca. Su distancia triádica es de hecho ⅓, pero el valor exacto no es lo más importante. Sí es importante que el 1 va a estar más cerca del 4 que del 2, el 3 o el 5. Veamos ahora el 7: tendremos que 7-1=6=2×3. Ignoramos el dos y nos quedamos con un tres, la misma potencia que en 4-1. Por tanto, el 7 está a la misma distancia del 1 que el 4.

Avancemos un paso más: veamos qué pasa con el 10. Tenemos que 10-1=9=3×3, y por tanto tenemos una potencia más alta: tres al cuadrado. Según la distancia triádica, el 10 está más cerca del 1 que el 4 o el 7; concretamente, la distancia entre ambos es 1/9. Supongo que ya empezáis a ver un patrón: 28-1=27=3×3×3, así que el 28 está todavía más cerca del 1. Y más cerca aún está el 82, ya que 82-1=81=3×3×3×3. En cambio, 136 está a la misma distancia del 1 que el 28, porque 136-1=135=5×3×3×3. Finalmente, vamos a ver alguna fracción: ¿será ⅔ un número cercano a 1? Tenemos que 1-⅔=⅓=3^(-1). Como esa potencia es negativa, la distancia entre ⅔ y el 1 es 3, la mayor de todas las que hemos calculado.

Todo esto parece una locura. Lo parece hasta que miramos las piezas de este puzle con unos ojos un poco diferentes: 1, 4 y 7 están a la misma distancia unos de otros según la métrica triádica. Y, curiosamente, 1+3=4 y 4+3=7. Lo mismo les pasa a 2, 5 y 8. O 3, 6 y 9. Parece que la métrica triádica agrupa “a la misma distancia” a los números que están separados por tres unidades. o por dos veces tres unidades (seis). Sin embargo, cuando la separación es de tres veces tres unidades, como el 1 y el 10, la métrica nos dice que esos números están más cerca. Aún más cerca están los que están separados por tres veces tres veces tres, como el 1 y el 28. La métrica triádica, en realidad, lo que está haciendo es estructurar los números en ciclos de tres, y esos ciclos los agrupa también en ciclos de tres, y ésos a su vez en otro ciclo de tres. Es una métrica sensible a las relaciones ternarias dentro de los números.

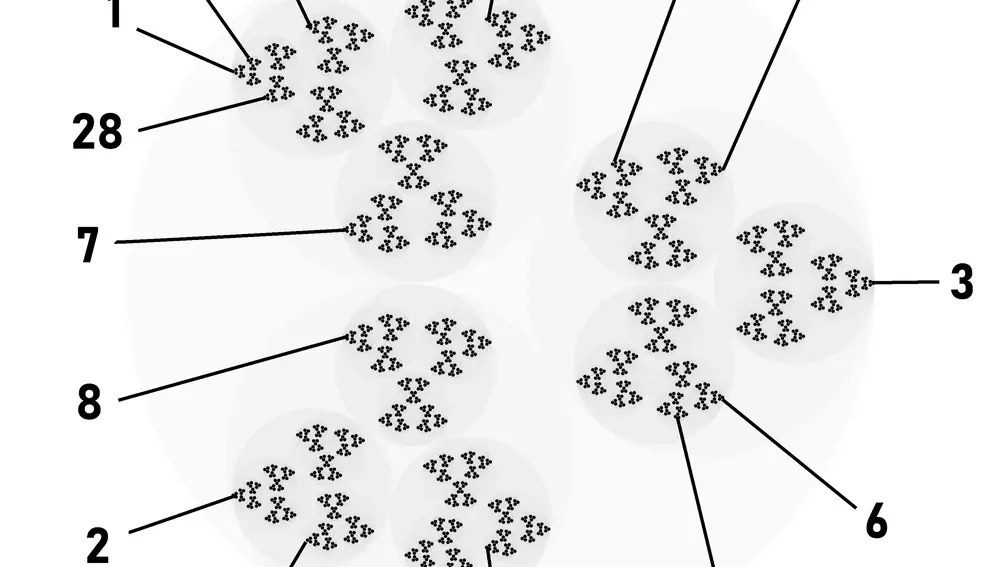
Las otras métricas p-ádicas van a comportarse de forma similar: la métrica diádica (p=2) es sensible a los ciclos binarios; la métrica pentádica (p=5), a los ciclos de cinco unidades, y de cinco veces cinco unidades… y así sucesivamente. Sin duda estas métricas no miden eso a lo que solemos llamar “distancia”, pero están midiendo algo. Se las compara a veces con la aritmética modular, porque parece que las cosas “se repiten al cabo de p unidades”, pero son más sutiles que eso: las métricas p-ádicas distinguen entre “p unidades” y “p² unidades”, cosa que no ocurre en la aritmética modular, y con ello son capaces de distinguir relaciones más complejas dentro del conjunto de los números.

Nuevos huecos, nuevos números

La existencia de estas formas alternativas de medir distancias sugiere que también puede haber formas alternativas de completar métricamente el conjunto de las fracciones. La secuencia {0.1, 0.12, 0.123, 0.1234, …}, que para la métrica real es convergente, no lo es para la métrica triádica: la distancia entre 0.12 y 0.1 es 1; la distancia entre 0.123 y 0.12 es ⅓; la distancia entre 0.1234 y 0.123 vuelve a ser 1. Desde el punto de vista de la métrica real tiene sentido colocar un número al final de esa secuencia; desde la óptica de la métrica triádica esa secuencia tiende a infinito.

Lo contrario también ocurre: la secuencia {1, 4, 13, 40, 121, 364, …} es divergente para la métrica real. En cambio, para la métrica triádica es una secuencia convergente que, claramente, no tiene una fracción al final: describe, por tanto, un “agujero” en las fracciones, al menos desde el punto de vista triádico. Curiosamente esta secuencia en concreto sólo será convergente para la métrica triádica; para todas las demás tiende a infinito.

El resultado de tomar las fracciones y rellenar todos los agujeros que “ve” una métrica p-ádica se llama números p-ádicos, y son conjuntos métricamente completos alternativos a los números reales. En ellos, números que a nuestra intuición le parecen muy lejanos pueden estar muy cerca, y secuencias que parecen tender a infinito en realidad terminan con un nuevo número, que es inimaginable desde la lógica de los reales. Los números p-ádicos son muy útiles en matemáticas, porque codifican relaciones entre los números enteros y los números primos y permiten estudiar relaciones cíclicas dentro de los números. Otro día hablaremos de sus aplicaciones, pero por hoy basta con que apuntemos que los números pueden funcionar de muchas maneras, y que “cerca” y “lejos” pueden tener significados muy sorprendentes.

QUE NO TE LA CUELEN

• Nociones como “distancia” y “tamaño” pueden definirse de muchas maneras en matemáticas, aunque para la mayoría de aplicaciones siempre usamos la definición habitual: la de la métrica real.
• Los números reales son abstracciones muy profundas, que surgen de exigir que cualquier secuencia convergente de fracciones tenga un número como límite. En comparación, los números enteros y racionales son objetos extremadamente sencillos e intuitivos.
• Los números p-ádicos son igual de fáciles o difíciles que los reales. Lo que ocurre es que tenemos mucho entrenamiento para pensar con la métrica real, y poco para pensar con las métricas p-ádicas.

REFERENCIAS

• Neal Koblitz. p-adic Numbers, p-adic Analysis, and Zeta-Functions. Springer (1977)
• Dmitri V. Chistyakov. Fractal geometry for images of continuous embeddings of p-adic numbers and solenoids into Euclidean spaces. Theoretical and Mathematical Physics, vol. 109, pp. 1495–1507 (1996)