El hotel que te ayuda a entender el infinito

Dicen las voces expertas que la ciencia nos da una manera de entender el mundo que nos rodea. Explica por qué no podemos andar por el techo, por qué llueve de vez en cuando o cómo un minúsculo virus puede revolucionar el mundo en pocos meses. Une los cabos de nuestra experiencia y es capaz de hacer predicciones sobre el futuro: si sueltas el teléfono en el que estás leyendo este artículo, se estrellará contra el suelo. Lo dice la ciencia.

Pero, a veces, la ciencia nos da sorpresas. En ocasiones las afirmaciones que hace entran en conflicto directo con nuestra experiencia. Yo nunca he visto un objeto que no esté ni aquí ni allí, sino en superposición de ambos sitios, a pesar de que sé, por la teoría cuántica, que eso ocurre todos los días. Soy demasiado grande para verlo de primera mano.

Entonces, ¿cómo aproximarnos a los fenómenos antintuitivos? Con experimentos mentales. Como con el gato de Schrödinger, se trata de imaginarnos situaciones en las que estos fenómenos ocurren a nuestra escala, y apuntar las consecuencias. Los gatos no pueden estar en superposición de vida y muerte, pero fantasear con esa posibilidad nos ayuda a entender la física.

Un hotel siempre completo

De hecho, los experimentos mentales son indispensables en matemáticas, donde ni siquiera podemos ir a ningún laboratorio a comprobar nada. Al igual que no podemos ver gatos en superposición, tampoco podemos ver el infinito. Podemos imaginar cantidades muy, muy grandes, pero ¿y las que nunca acaban?

Por fortuna, el hotel infinito que propuso David Hilbert en 1924 nos ayuda. Es un hotel que tiene un número infinito de habitaciones, numeradas correlativamente: 1, 2, 3, y así sucesivamente. En temporada alta, el hotel está siempre completo.

Pero imaginemos que llega una persona más pidiendo alojamiento. La tentación de reconvertir un armario en habitación cápsula improvisada es grande… pero dañaría la reputación del hotel. En un hotel normal, la persona se quedaría fuera. Pero el hotel de Hilbert es infinito.

¿Cómo alojar al nuevo huésped? La idea es sencilla: se le pide a la persona que ocupa la habitación 1 que se traslade a la habitación 2. A quien ocupa la habitación 2 se le traslada a la 3, el de la 3 pasa a la 4, y así sucesivamente. Es decir, la persona de la habitación n se traslada a la n+1. Como el hotel no tiene fin, nadie se queda sin habitación a la que ir. De este modo, la habitación 1 queda libre para la nueva persona.

Si en lugar de una persona llegaran tres, 47 o 525, podríamos emplear el mismo método: cada persona se traslada tres, 47 o 525 habitaciones más allá, dejando libre el número justo de habitaciones para acomodar a las recién llegadas.

Muñecas rusas

Pero, ¿y si llegara un autobús turístico con infinitas personas más? Afortunadamente, el hotel de Hilbert también las puede acomodar. El truco de mover a cada persona del hotel unas cuantas habitaciones más allá ya no funciona, pero el hotel de Hilbert no se rinde.

En vez, trasladamos a la persona de la habitación 1 a la 2, la de la 2 a la 4, la de la 3 a la 6, y así sucesivamente. Es decir, la persona de la habitación n pasa a la habitación 2n. De este modo, todas las habitaciones impares quedan libres, y hay sitio para acomodar al autobús al completo.

Pero la situación se podría complicar todavía más: supongamos que el hotel está en la costa. Ahora, llega un barco con infinitos autobuses turísticos, cada uno de los cuales tiene infinitas personas. Una especie de muñeca rusa de infinitos. ¿Se pueden alojar en el hotel?

A lo mejor ya intuyes que sí. Efectivamente, no hay problema en alojarlas, solo tenemos que encontrar una forma de trasladar a las ocupantes actuales del hotel a habitaciones distintas, dejando huecos suficientes para acomodar a las infinitas personas de los infinitos autobuses del barco.

Para lograrlo, escribimos los números naturales (es decir, 1, 2, 3, etc.) en forma de pirámide. En la primera fila escribimos solo el 1. En la segunda, el 2 y el 3. En la tercera, el 4, el 5 y el 6, y así sucesivamente.

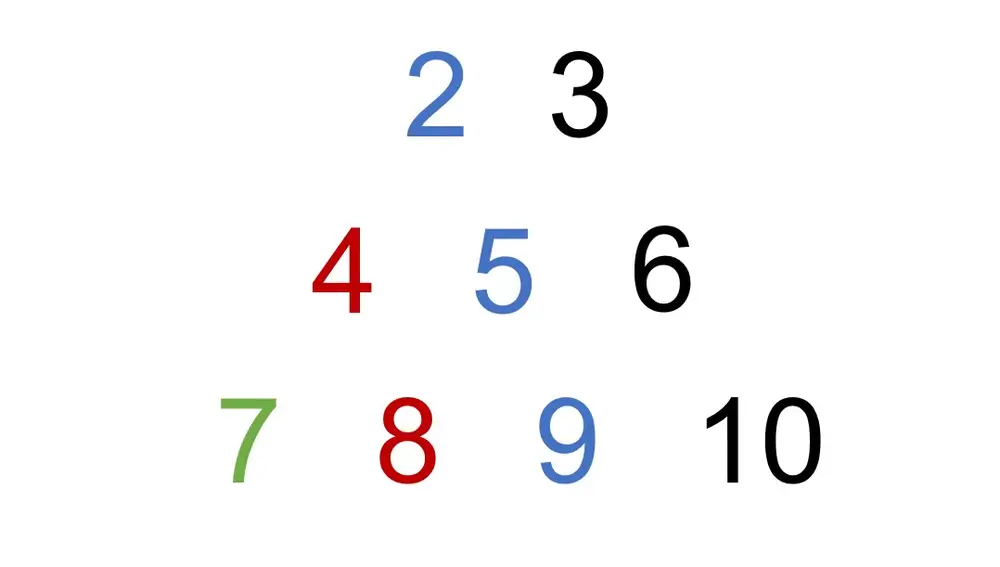
Pirámide de números para alojar un barco lleno de infinitos autobuses, cada uno con infinitas personas. La Razón.

Vemos que, si empezamos por la cúspide y recorremos la diagonal de la derecha, se forma una sucesión de números, 1, 3, 6, 10, 15… A cada ocupante original del hotel le asignaremos una habitación de esa lista, en orden correlativo. La persona de la habitación 1 se quedará donde está, la de la 2 pasará a la 3, la de la 3 a la 6, y así sucesivamente.

Si seguimos el mismo recorrido (diagonal hacia abajo) empezando por el número 2, tendremos la sucesión 2, 5, 9, 14… En esta fila colocamos a las personas que venían en el primer autobús, también en orden correlativo. En la sucesión siguiente (4, 8, 13…) colocamos al segundo autobús, y así sucesivamente.

Una habitación para cada huésped

Puesto que la pirámide nunca acaba, hay tantas sucesiones de números como autobuses. Y, por la forma en la que hemos diseñado la pirámide, sabemos que no se repite ningún número, de modo que hay una persona en cada habitación y una habitación para cada persona. El hotel de Hilbert vence de nuevo.

Este es un ejemplo de una paradoja verídica, es decir, una situación que conduce a un resultado antintuitivo, pero que podemos demostrar que es cierto. En los hoteles infinitos, no es equivalente decir que todas las habitaciones están ocupadas y que no se admiten más huéspedes.

En el fondo, los números naturales, por familiares que parezcan, tienen consecuencias inesperadas que no podemos experimentar de primera mano. Aunque nunca nos vayan a contratar como recepcionistas del hotel de Hilbert, este experimento mental nos ayuda a entender cómo se comportan los números naturales. En definitiva,

QUE NO TE LA CUELEN:

• El hotel de Hilbert no es todopoderoso: hay grupos de personas que se le resisten. Imaginemos que llegara un autobús con un asiento por cada número real. Un autobús que, en lugar de tener asientos 1, 2, 3, etc., tuviera asientos con decimales, incluso con ristras infinitas de decimales que nunca se repiten. En este autobús, la raíz cuadrada de dos, el número pi y el número áureo tendrían su asiento. Pues bien, para este autobús no habría acomodo posible en el hotel de Hilbert. La razón es que el conjunto de los números reales es no numerable. Es decir, es imposible asociar un número natural a cada número real. Hay infinitos números naturales e infinitos reales, pero el infinitos de los reales es aún más grande que el infinito de los naturales.

REFERENCIAS (MLA):

• Ewald, William, and Wilfried Sieg, editors. David Hilbert’s Lectures on the Foundations of Arithmetic and Logic 1917-1933. Springer Berlin Heidelberg, 2013. https://doi.org/10.1007/978-3-540-69444-1