¿Puedes resolver este problema geométrico?

La pandemia todavía no ha pasado, aunque claramente estamos mejor que hace un año. Por aquel entonces, muchos países estaban viviendo sus peores momentos hasta entonces. No obstante, habíamos dejado atrás las primeras semanas donde, con tal de no pensar en el asfixiante encierro, algunos bailaban desde los balcones o salían a aplaudir algo que ya no parecen recordar. Y mientras muchos de nosotros zangolotineábamos de una habitación a otra, dos matemáticos se enfrentaron a un problema tan sencillo de plantear como imposible de resolver. Un pariente cercano del cuadrado inscrito.

Sus nombres eran Joshua Greene y Andrew Lobb y su propósito, demostrar si podemos dibujar todos los rectángulos posibles sobre cualquier curva cerrada sobre sí misma colocando siempre las esquinas sobre la propia curva. Toma lápiz y papel e inténtalo antes de seguir leyendo. ¿Crees que sabes la respuesta?

Los actos no demuestran nada

En la vida real las palabras se las lleva el viento y lo único que demuestra qué sentimos y opinamos son nuestros actos. En matemáticas ocurre lo contrario. Podemos intentar crear cientos de rectángulos diferentes en un garabato creado al azar, pero eso no demostrará nada más profundo, solo que hemos podido dibujar cierto número de rectángulos sobre un garabato concreto. Para demostrar algo de verdad la matemática tiene que, por ejemplo, partir de las afirmaciones que sabemos que son ciertas y demostrar que, para no caer en contradicciones, hemos de aceptar o rechazar la nueva conjetura que estábamos estudiando.

Por supuesto, otra opción es encontrar un contraejemplo. Un caso en que tu conjetura no se cumpla es suficiente para que sea rechazada o, en todo caso, limitada a casos particulares. Precisamente por eso es tan complicado demostrar algunas conjeturas matemáticas, por sencillas o intuitivas que parezcan. Así surgen famosas conjeturas como las de Collatz, la ABC o la de Goldbach. Pues en esa misma línea surgió en 1911 la conjetura de Toeplitz, el padre de lo que hoy nos trae aquí.

El problema del cuadrado inscrito

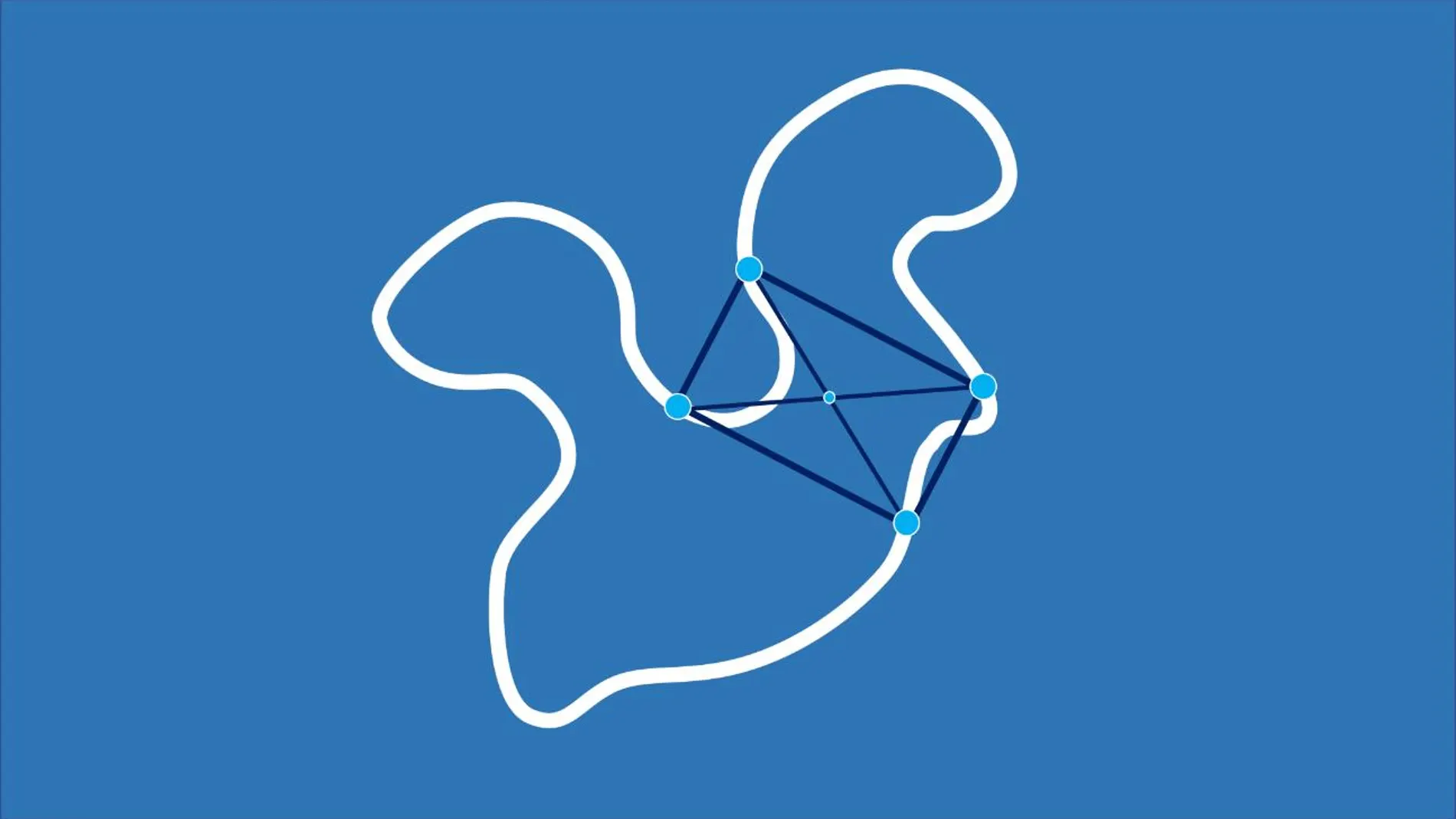
Su otro nombre es mucho más pronunciable y da pistas sobre su naturaleza: el problema del cuadrado inscrito. Lo que Toeplitz planteó en 1911 fue si toda curva de Jordan admite un cuadrado inscrito. Puede que suene amenazador, pero aclarando un par de conceptos se vuelve realmente sencillo. Una curva de Jordan es un garabato plano cuyos extremos están unidos. Puede tener esquinas o ser totalmente suave, lo que sí es obligatorio es que sea continua. Que el cuadrado esté inscrito significa que sus esquinas han de tocar cada una un punto del perímetro del “garabato”.

Pues bien, por sencillo que parezca, este problema sigue sin solución. No ha sido demostrado, por mucho que tampoco conozcamos contraejemplos. Dicen que cuando a un ingeniero se le presenta un problema demasiado complejo suele dividirlo en problemas más pequeños y sencillos de resolver. En cambio, cuando un matemático se encuentra en esta tesitura lo que hace es enfrentarse a casos particulares. Por ejemplo, en 1929 se demostró que, efectivamente, podía dibujarse un cuadrado inscrito en toda curva de Jordan mientras esta cumpliera el caso particular de ser suave. Lo cual significa que no tenga aristas en ella, sino que sea “redondeada”. Esto no demuestra la conjetura de Toeplitz, pero sí demuestra una parte.

Esos pasos no significan necesariamente que la conjetura inicial tenga más posibilidades de ser cierta, pero pueden ayudar a comprender la conjetura y desarrollar herramientas nuevas para demostrarla. Pues bien, lo que Greene y Lobb han querido hacer es resolver uno de esos casos particulares. El problema del rectángulo.

Cuestión de proporciones

Estos matemáticos decidieron preguntarse si, para una curva cerrada, continua y suave cualquiera, podemos dibujar cualquier rectángulo imaginable. Y cuando decimos “cualquier rectángulo imaginable” hablamos de la proporción entre sus lados. Si lo pensamos, ya hemos confirmado que puede ser posible al menos un rectángulo, concretamente un caso particular de rectángulo cuyos lados son iguales, vamos, lo que solemos llamar cuadrado. La idea ahora es extender esto a cualquier rectángulo, desde los más finos hasta los que casi parecen cuadrados.

Lobb y Greene ya perseguían esta conjetura antes de la cuarentena, pero el tiempo que esta les proporcionó ha hecho posible lo que ellos creían poco probable: demostrarla. A riesgo de destripar la historia, diremos que han sido capaces de demostrar su conjetura y ahora sabemos que, mientras la curva sea cerrada continua y suave, podemos rectángulos de cualquier proporción imaginable.

El proceso mediante el que han conseguido demostrar la conjetura es complicado de transmitir con precisión en pocas palabras, entre otras cosas porque implica figuras en cuatro dimensiones espaciales. De hecho, el siguiente bloque es bastante abstracto incluso habiendo sido simplificado, por lo que siempre puedes continuar directamente al último párrafo.

Dimensiones para valientes

En cualquier caso, podemos decir que han partido de una idea ya clásica, y es que un rectángulo puede definirse como dos pares de puntos (cada uno una esquina) cuyas diagonales miden lo mismo y se cruzan en el centro. Si tomamos esta idea y queremos representar en un gráfico todos los pares de esquinas posibles, lo que podemos hacer es cortar la curva en un punto, estirarla y usarla para representar los ejes horizontal y vertical de un sistema de coordenadas. Al hacer esto y representar cada punto del eje horizontal, aparejado con un punto del eje vertical, veremos que el plano entero se llena de infinidad de puntos, formando un cuadrado. No obstante, este cuadrado tiene una peculiaridad. Al haberse creado a partir de una curva que hemos roto, los lados del cuadrado, al igual que los extremos de la curva, pueden volverse a unir. Y no de cualquier manera, porque para respetar el planteamiento de la conjetura el cuadrado debe plegarse de forma que, en lugar de obtener un cilindro, como cuando rizamos una hoja de papel, conseguimos una estructura mucho más extraña: una cinta de Möbius.

La cinta de Möbius es una figura de tres dimensiones, pero con un único lado. Algo así como si cortáramos una tira de papel rectangular y uniéramos sus extremos tras girar uno de ellos 180º sobre su eje longitudinal. Si ponemos el dedo sobre él y lo vamos moviendo veremos que repasaremos las dos superficies del papel original como si fueran la misma.

Y ahora es cuando la cosa se pone realmente compleja de visualizar, porque los matemáticos decidieron colocar esa misma cinta de Möbius, no en un espacio tridimensional, sino en cuatro dimensiones espaciales. Para eso necesitaban que cada punto de la cinta estuviera definido por cuatro coordenadas, al igual que nosotros nos localizamos en nuestras tres dimensiones con altura, anchura y profundidad. Así pues, tomaron como los dos primeros son las dos coordenadas del punto medio de cada par de puntos posibles en la curva. La tercera coordenada estaba definida por la distancia entre cada uno de esos dos puntos. Finalmente, la cuarta era el ángulo que forma la línea que une ambos puntos con el eje horizontal.

Tras representar la cinta en un espacio de cuatro dimensiones (concretamente un espacio simpléctico de cuatro dimensiones) comenzaron a estudiar cómo se solapaba la cinta consigo misma si creaban una copia y la rotaban solo en su última coordenada. Por ejemplo, nosotros podemos girar la cabeza en las tres direcciones del espacio, pero cuando asentimos solo la movemos de arriba abajo. Ni de un lado a otro, ni de delante a atrás. Y aquí está la clave final. Cuando la cinta de Möbius original y la rotada se cortaban en algún punto, la ubicación de la intersección indicaba las coordenadas que tendrían en la cinta los dos pares de puntos de un rectángulo inscrito. Pues bien, Lobb y Greene demostraron que no había forma de rotar la segunda cinta de Möbius en ese espacio simpléctico de cuatro dimensiones sin que estas se solaparan, o, dicho de otro modo: siempre iba a haber puntos con los que confeccionar un rectángulo, no importa la inclinación que tuvieran esos pares de puntos entre sí (la última coordenada).

Un matemático entra en un bar

Cuenta un chiste que un matemático y un físico se encontraron en una conferencia sobre espacios de nueve dimensiones. El matemático sigue las explicaciones con entusiasmo, pero a medida que la charla avanza, el físico se siente cada vez más perdido. Pasado un tiempo, sorprendido por lo atento que está su compañero, el físico decide preguntarle al matemático cómo es capaz de entender ese galimatías de nueve dimensiones. El matemático le responde que tan solo tiene que representarlo en su cabeza, lo cual desconcierta todavía más al físico, que replica molesto “Nadie puede visualizar nueve dimensiones”. Y entonces, el matemático responde: “Claro que sí, solo tengo que imaginar un espacio de X dimensiones y luego hacer X igual a nueve”.

Nunca dije que fuera un buen chiste, pero desde luego, representa bastante bien la normalidad con la que los matemáticos se acercan a este tipo de conceptos que se escapan a cualquier cosa imaginable por la mente humana. En caso de tener que visualizar un objeto de más de tres dimensiones, tienen trucos para proyectarlo en nuestras intuitivas tres dimensiones, solo que añadiéndoles algunas propiedades cuasimágicas. Un ejemplo es la botella de Klein, que no deja de ser dos cintas de Möbius unidas. Cuando la representamos en cuatro dimensiones veremos una botella cuyo cuello se curva, atraviesa uno de sus propios laterales y desde “dentro” de la botella forma un embudo que conecta con la base. No obstante, para ser una botella de Klein tendríamos que dar un pequeño salto de fe e imaginar que es capaz de conectarse de ese modo sin tener que atravesarse a sí misma en ningún punto. Algo trivial en las cuatro dimensiones de las que es originaria, pero inviable en nuestro mundo.

Pues bien, resulta que hay otro espacio donde la botella de Klein se corta consigo misma y se trata de un espacio simpléctico de cuatro dimensiones. Teniendo en cuenta que dos cintas de Möbius que no se intersequen entre sí equivalen a una botella de Klein que no se atraviese a sí misma y esta es imposible en un espacio simpléctico de cuatro dimensiones llegamos a la contradicción que necesitamos para demostrar algo en matemáticas. La única solución posible es que haya infinitos rectángulos inscritos en una curva cerrada, porque de otro modo, tendría que haber rotaciones de la segunda cinta de Möbius que la cortaran con al original, y ahora sabemos que eso no es posible.

En cualquier caso y tras tanto texto, esta historia de cuadrados y curvas nos cuenta cómo surge la necesidad de utilizar una cuarta dimensión del espacio. Porque lejos de ser trucos de magia o una suerte de fuegos artificiales, trabajar con dimensiones extra es una de las mayores fortalezas de las matemáticas y de las que hace de ellas una herramienta tan poderosa para entender el mundo.

QUE NO TE LA CUELEN:

• Históricamente hemos relacionado la cuarta dimensión con el tiempo, lo cual es correcto, pero en este caso hablamos exclusivamente de dimensiones espaciales. Al referirnos a la cuarta no pretendemos hacer ninguna referencia al tiempo.
• Hablar de otras dimensiones tampoco implica referirnos a fenómenos sobrenaturales, fantasmas o universos paralelos. No tiene nada que ver y es conveniente no confundir estos conceptos.

REFERENCIAS (MLA):

• GREENE, JOSHUA EVAN, and ANDREW LOBB. “THE RECTANGULAR PEG PROBLEM”. 2020, https://arxiv.org/pdf/2005.09193.pdf. Accessed 18 July 2020.